MUHAMMET ARICAN

NAPOLEON THEOREM

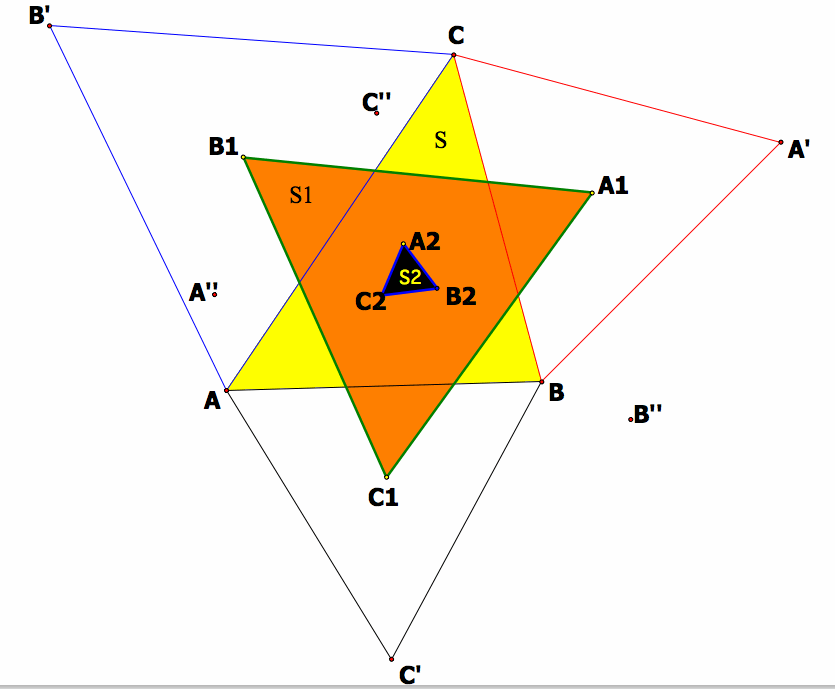
This theorem named after Napoleon Bonaparte who was an Emperor of the French Empire and he also interested with mathematics. He explained that if we construct equilateral triangles on the sides of any triangle, the centers of those equilateral triangles themselves form an equilateral triangle, as I illustrated below inner and outer Napoleon triangles are both equilateral triangles.

Inner Napoleon Triangle:

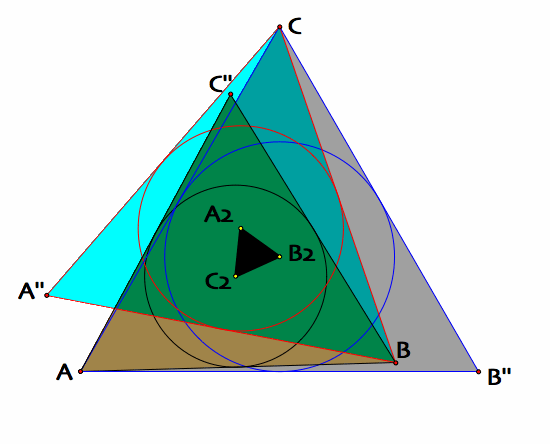
GSP for inner Napoleon triangle

Outer Napoleon Triangle:

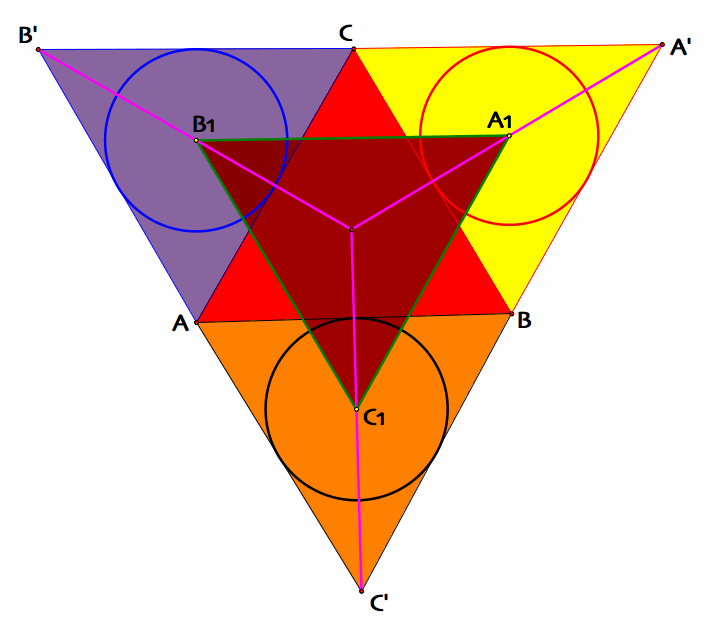
GSP for outer Napoleon triangle

Napoleon Theorem:

This theorem states that both inner Napoleon and outer Napoleon triangles are equaleteral triangles. Now let give a proof for this statement:

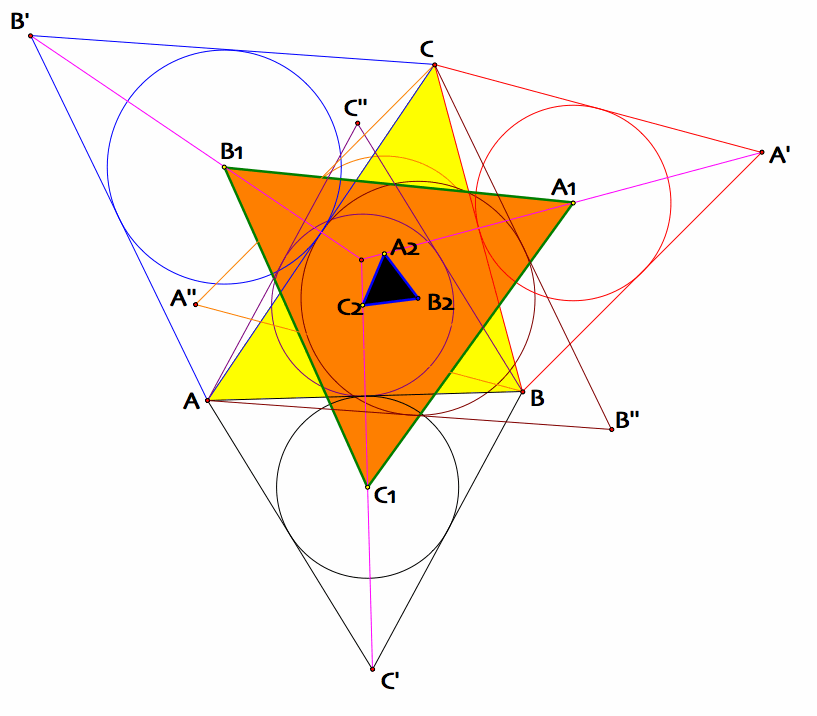
A picture for Napoleon triangles

GSP for Napoleon Theorem

Proof for Outer Napoleon triangle:

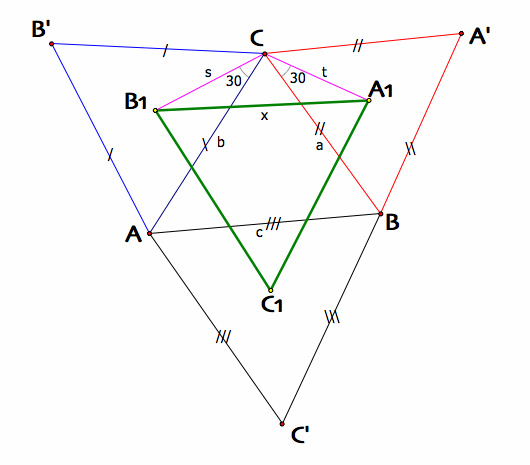
From Law of Cosines x² = s² + t² - 2st.cos(C + 60). (a)

Since, we know the centroid of a triangle lies along each median and 2/3 of the distance from the vertex to the midpoint of the opposite side, we have

t = (2/3).√3/2. a = a /√3

s = (2/3).√3/2 . b = b/√3, if replace t and s in (a) then we (a) becomes

x² = b²/3 + a²/3 - 2ab/3.cos(C + 60) <=> 3x² = b² + a² - 2ab.cos(C + 60). (b)

and cos(C+60) = cos C.cos 60–sin C . sin 60 = cos C . 1/2 –sin C . √3/2. (c)

Substituting (c) into (b) gives

3x² = b² + a² - ab.cos(C) + √3.ab.sin (C). (d)

Now if we apply Law of Cosines to ABC triangle then we will have

c² = a² + b² –2ab cos (C) (e)

and from Law of Sines

A(ABC) = ab.sin(C)/2 => 2A(ABC) = ab.sin(C). (f)

If we substitute (e) and (f) into (d) then we will have

3x² = 1/2( a²+b²+c²) + 2 √3. Area(ABC). (g)

Since (g) is symmetrical in a, b, and c, so the triangle connecting the three centroids is equilateral.

Proof for Inner Napoleon triangle:

Proof for inner Napoleon triangle is similar with outer Napoleon triangle. If we call y the length of one side of inner Napoleon triangle

then we can show 3y²= 1/2( a²+b²+c²) - 2 √3. Area(ABC) as I showed above for outer Napoleon triangle thus the inner

Napoleon triangle is an equilateral triangle also.

Now, I can give an interesting result of Napoleon theorem:

The Area of ABC triangle = The area of Outer Napoleon triangle - The area of Inner Napoleon triangle

S=S1-S2

Proof for this result:

As we know the area of any equilateral triangle = square of one side . √3/4. Now

S1= x² √3/4 and S2= y² √3/4

also from above

3x² = 1/2( a²+b²+c²) + 2 √3. Area(ABC)

Now, if we multiply both sides by √3/12 then we can get

x² √3/4 = S1 = √3/24 (a²+b²+c²) + 1/2 Area(ABC)

and similarly if we do the same for 3y² then we will get

y² √3/4 = S2 = sqrt3/24 (a²+b²+c²) - 1/2 Area(ABC).